|
『科学談話室』の話題より | ||
| この話題は 光を光速で追う からの続きです | ||
| [danwa:0101] 光行差・ドップラー効果と波面(Aberration) | |||
| Date:Sat, 25 Dec 1999 11:01:18 | From: 石坂 | ||
|
浜口さま、談話室のみなさま、こんにちは。 光行差について、 [danwa:0094]浜口さんは書きました。
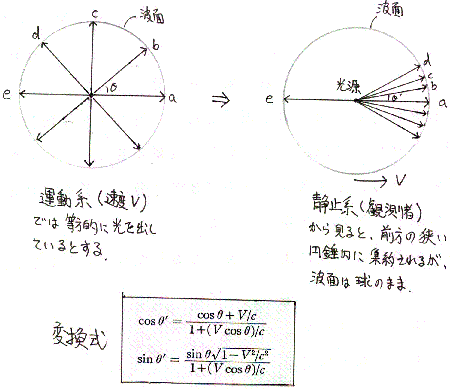
今考えているのは球面波ですので、「波面の傾きがかわ」ったからといって、 波面は変わりません。方向の変換は sin, cos だけですから…。 また、光行差はドップラー効果とは関係なく求められるものです。 光行差には波面間隔は関係ないので、
石坂 | |||
| [danwa:0105] Re: 光行差・ドップラー効果と波面 | ||||
| Date:Sun, 26 Dec 1999 13:27:05 | From: 浜口 | |||
|
石坂さん,こんにちは. 浜口です. ([danwa:0101]石坂さん)
光線の向き ↑ 光線の向き ――― \ ♂ ―――波面群 \ \ ――― \ \ \ ――― \ \ \ 波面群 光線の向きが違えば,波面の傾きも変わります. まずここまではよいでしょうか. (これがOKなら,次は,球面波の図の話にうつります) 浜口 | ||||
| [danwa:0106] Re: 光行差・ドップラー効果と波面 | |||
| Date:Sun, 26 Dec 1999 13:40:56 | From: 石坂 | ||
浜口さん、談話室のみなさま、こんにちは。石坂です。
| |||
| [danwa:0108] Re: 光行差・ドップラー効果と波面 | |||
| Date:Sun, 26 Dec 1999 16:33:06 | From: 浜口 | ||
|
浜口です. ([danwa:0107]石坂さん)
では,続けます. (いまの議論の当面の目標は,光行差を波面の変化として説明すること,でい いですよね) 波長λ0の光 (振動数でいえばν0=c/λ0)を出す点光源を考えます. 慣性系をひとつとって「S系」と呼んでおきます. 光源は,S系のx方向に一定速度vで運動しているとします. 光源に固定した座標系を「S'系」と呼んでおきます. (x,y,z軸とx',y',z'軸はそれぞれ平行とします.ローレンツ変換 式を出すときの,よくある設定ですね) するとS'系では,ある瞬間の波面は,次のようになっています. (光はあらゆる方向に進んでいますが,x'軸上とy'軸上の波面だけ描きまし た) y' ↑ ――― ―――波面間隔λ0 ――― ――― |||| |||| |||| ◎ |||| →x' |||| 光源 |||| 波面間隔λ0 波面間隔λ0 ――― ――― ―――波面間隔λ0 ――― ここまではよいでしょうか. 浜口 | |||
| [danwa:0109] Re: 光行差・ドップラー効果と波面 | |||
| Date:Sun, 26 Dec 1999 17:21:11 | From: 石坂 | ||
|
石坂です。 [danwa:0108] 浜口さん:
| |||
| [danwa:0110] Re: 光行差・ドップラー効果と波面 | |
| Date:Sun, 26 Dec 1999 23:13:37 | From: 浜口 |
|
石坂さん,こんばんは. 浜口です. では続けますね. (イメージの話はあとまわしにして,先に計算でやってしまおうと思います) y' ↑ ――― ―――[2] ――― ――― [1] |||| |||| |||| ◎ |||| →x' |||| 光源 |||| S'系で,[1]の波(正弦波としておきます)を式で表すと, 2π Ψ=Asin ――(x'−ct') ……【1】 λ0 となります. 単に,x'方向に速度cで進む波長λ0の平面波の式です. (波面は厳密には球面の一部だが,x'軸の周辺だけなら平面波とみなせる) 同様に[2]の波を式で表すと, 2π Ψ=Asin ――(y'−ct') ……【2】 λ0 となります. よろしいでしょうか. 浜口 | |
| [danwa:0113] Re: 光行差・ドップラー効果と波面 | ||
| Date:Tue, 28 Dec 1999 09:04:26 | From: 石坂 | |
|
浜口さま、談話室のみなさま、こんにちは。 石坂です。 [danwa:0110]浜口さん:
| ||
| [danwa:0114] Re: 光行差・ドップラー効果と波面 | |||
| Date:Tue, 28 Dec 1999 16:06:18 | From: 浜口 | ||
浜口です.
あとは(予想されているとおり)ローレンツ変換でS系に移り,波の式がS系 でどのようになっているかを観察するだけですから. 浜口 | |||
| [danwa:0116] Re: 光行差・ドップラー効果と波面 | |||
| Date:Tue, 28 Dec 1999 17:51:41 | From: 石坂 | ||
|
浜口さま、談話室の皆さま、こんばんは。石坂です。 [danwa:0114] 浜口さん:
はたして、正弦波をローレンツ変換すれば、光行差が球面波を球面波でなくする、こ とが理解できるかな・・・?(今は信じられないけど) 談話室のみなさま、よいお年をお迎えください。 ところで、過去のログを読んでいて、 [danwa:0083]浜口さん:
みなさんは本当に宇宙船が崩壊すると思いますか? | |||
| [danwa:0125] Re: 光行差・ドップラー効果と波面 | |
| Date:Wed, 5 Jan 2000 23:19:45 | From: 石坂 |
|
談話室のみなさま、明けましておめでとうございます。 石坂@科学館です。 本年もよろしくお願いいたします。 さて、私には正月休みの宿題が出ていました。 「慣性系Sに対して速度V(一定)で x軸+方向に走るS'系にある光源 がS'系でx'軸+方向(1)、y'軸+方向(2)、x'軸−方向(3)、y'軸 −方向(4)に平面波を出しているとき、S系ではどのように観測されるか」 ([danwa:0110]、[danwa:0114]浜口さん) というものでした。 4方向でそれぞれ計算すると絶対計算間違いをすると思ったので(^^) 波の進む方向を示す単位ベクトル(nx'、ny')を 使って波Ψ'を 2π Ψ'=A'sin――(nx'・x'+ny'・y'−ct') …(式1) λ0 と書きます。(1)の波は(nx',ny')=(1,0)、 (2)(3)(4)は それぞれ、 (0,1)、(-1,0)、(0,-1)です。任意の方向へ進む波は、x'軸からの角度をθ'とし て、(nx',ny')=(cosθ',sinθ')で表せます。 この波がS系で 2π Ψ=Asin――(nx・x+ny・y−ct) …(式2) λ として観測されたときのλ、nx、nyを求めます。 (式1)に S系→S'系 のローレンツ変換の公式 x'=γ・(x−Vt) y'=y ct'=γ・(ct−Vx/c) を代入します。ここで _____________ γ=1/√(1−V2/c2) です。 x、y、tについて項をまとめると、Ψ'の位相部分は 2π ――(nx'・x'+ny'・y'−ct') λ0 2π =――・γ・(1+nx'・V/c) λ0 nx'+V/c ny'/γ ・(――――――x +――――――y -ct) 1+nx'・V/c 1+nx'・V/c と書けます。 これを(式2)の位相部分と比較すると、 λ0 λ=――――――――― …(式3) γ・(1+nx'・V/c) nx'+V/c nx=―――――――― …(式4) 1+nx'・V/c 1/γ ny=――――――――・ny' …(式5) 1+nx'・V/c が得られました。(式3)(式4)(式5)の解釈については、次号につづく・・・ | |
| [danwa:0129] Re: 光行差・ドップラー効果と波面 | |
| Date:Fri, 7 Jan 2000 22:00:29 | From: 石坂 |
|
談話室のみなさん、こんばんは。石坂です。 式が続きますが、ご容赦ください。今回も長文ですが、まだまだ先は長いなー・・・ (;_;)。 前回[danwa:0125]の結果得られた、S'系→S系 での波の変換式のうち、 λ0 λ=――――――――― …(式3) γ・(1+nx'・V/c) は運動によって波長が変わることを示しています。これが相対論的なドップラー効果 の式です。 そして、波(光線)の進行方向の変化を示す以下の2式が、今注目している光行差 の式になります。 nx'+V/c nx=―――――――― …(式4) 1+nx'・V/c 1/γ ny=――――――――・ny' …(式5) 1+nx'・V/c これらの式で波(1)や波(2)の場合を考えてみます。 x'軸+方向に放射された波(1)の方向ベクトル (nx',ny')=(1,0)を代入する と、(式4)、(式5)から(nx,ny)=(1,0)が得られます。 一方向に出た(3)の波(-1,0)も同様で、(nx,ny)=(-1,0) となります。 つまりx'軸方向に出た波は、慣性系Sで見てもx軸方向に出ていて、波(光 線)の方向は変わっていません。 さて、y'軸方向の波はどうでしょうか。 (2)の波(0,1)を(式4)、(式5)に代入すると、次のようになります。 nx=V/c ny=1/γ もし光源の速さVが光の速度cの50%なら、S系ではy軸よりも30度前方に傾 いて出てくることになります!(4)についても同様。 光線(波)の方向が変わっています。 「任意の速度Vで走る慣性系S'の光源がy'方向に出す光は、S系ではその速度 に応じて前方に傾いて放射されるように観察される。」 ところで、任意の方向へ進む波は、x'軸からの角度をθ'として、 (nx',ny')=(cosθ',sinθ')で表せました。 ここで(式4)と(式5)をそれぞれ二乗して足してみます。すると、あら不思議! nx・nx+ny・ny=1 です。つまり、ローレンツ変換を行った後の方向ベクトル (nx,ny)も単位ベクトル(長さが1のベクトル)です。 そこで、x軸からの角度をθとして、 (nx,ny)=(cosθ,sinθ)と書き表すと、 (式4),(式5)の2式は[danwa:0101]で 石坂が教科書からひっぱってきた光行差の式と同じものになります (ただし、’の付け方が今回の設定と逆になっていることに注意してください)。 ここまでをまとめておきます。
さて、次回はいよいよ球面波の場合に行きたいと思います。 みなさま、おやすみなさい。 | |
| [danwa:0131] Re: 光行差・ドップラー効果と波面 | |||
| Date:Sat, 8 Jan 2000 01:28:24 | From: 浜口 | ||
|
浜口です. 談話室のみなさんあけましておめでとうございます. 本年もよろしくお願いいたします.m(__)m ([danwa:0125]石坂さん)
むしろ私だったら,一般的にやると絶対計算間違いをしそうなので,逆に, 結果の予想できる特殊な場合を試しに計算してみるところです. (それが,簡単な平面波の式を提示させていただいた理由でした) ま,個人の好みの問題なので,どちらがどうということはありません.(^^ゞ それはさておき,計算おつかれさまでした.OKです.石坂さんの計算あっ てると思います.(^_^)(^_^)(^_^) (正月に宿題なんか出してごめんね) 以下,(読者のみなさんのために)簡単に解説しておきます. まず(式1)は,一般の方向に光速で進む平面波を表しています. → \ n \ \ ♂ 波面の単位法線ベクトル \ \ \ (長さ1で波面に垂直) \ \ \ \ \ \ \ \ y’ \ \ \ ↑ \ \ 間隔λ0の波面群 →x’ \ → ベクトルnの成分を(nx',ny')と書いてあります. 長さ1なので「nx'とny'の2乗の和=1」 となっています. この(式1)はS'系で記述されています.この状況をS系で記述するとどうなるか, が知りたいことがらです. そのために,おなじみのローレンツ変換式(どんな本にも出てる式) x'=おなじみの式 y'=y t'=おなじみの式 を(式1)のx',y',t'に代入します. するとx',y',t'のかわりにx,y,tを含む式が得られます. それを整理すると,次のような,石坂さんの導かれた式が出てきます. (位相の部分(sinの中身の部分)だけ書いてあります) ([danwa:0125]石坂さん)
このx,yの係数が「S系での波面の単位法線ベクトルの成分」となります. (余談ですが,このように変形すると,tの係数が自動的にcになります.波 面が(S系においても)速度cで進むことを表しています.光速度不変の原理と 合ってます.ローレンツ変換ってほんとにうまくできてますねー) あとはこの式を,S系での式(位相部分) 2π ――(nx・x+ny・y−ct) λ と見比べることによって, 「S系での波長λとS'系での波長λ0との関係」 「S系での法線ベクトル(nx,ny)とS'系での法線ベクトル (nx',ny')との関係」 を知ることができます.それが結論です. 結果は石坂さんの計算どおり,[danwa:0125]の (式3),(式4),(式5)になります. 「ドップラー効果」(波長の変化(波面間隔の変化)と「光行差」(波の方向の変 化(波面の傾きの変化)」とが,ローレンツ変換による波面の変化として,一括 して統一的に導かれる. ということがおわかりいただけたでしょうか. 浜口 P.S. この計算が難しいと感じるかたは,[danwa:0110]の 【1】【2】式にローレン ツ変換式を代入してみて下さい.計算の感触がつかめると思います. | |||
| [danwa:0132] Re: 光行差・ドップラー効果と波面 | ||
| Date: Sat, 8 Jan 2000 01:31:57 | From: 浜口 | |
|
浜口です. ([danwa:0129]石坂さん)
なんで論旨がひっくりかえってるんですか. 実際に波面の方程式にローレンツ変換をおこなって結果(ドップラー効果と 光行差)を導いたのは,ご自身でしょ. 浜口 | ||
| [danwa:0134] Re: 光行差・ドップラー効果と波面 | |||
| Date:Mon, 10 Jan 2000 22:12:27 | From: 石坂 | ||
|
こんばんは、石坂です。 [danwa:0131]浜口さん:
[danwa:0132]浜口さん:
*ところで、[danwa:0101]の光行差の式は波面の変換から 求めたものではありませ ん。もっと横着に、速度のローレンツ変換の公式そのものから簡単に出ます(教科書 もだいたいこの方法を使っています)。 速度のローレンツ変換の公式: vx=(vx'+V)/(1+V・vx'/c2) vy=vy'/γ/(1+V・vx'/c2) に、vx=c・cosθ、vy=c・sinθ、 vx'=c・cosθ'、vy'=c・sinθ'を代 入するだけです(波面をローレンツ変換するのに比べて何て簡単なんだ!)。 でも、波面をローレンツ変換することで、ドップラー効果も一緒に考えることがで きて、なかなか有意義な正月休みでした ;−)。 さて、懸案の球面波を考えます。 S’系での波の式 2π Ψ'=A'sin――(nx'・x'+ny'・y'−ct') λ0 (ただし、nx'=cosθ'、ny'= sinθ') で、同時刻に位相が同じになるような(x',y')は、つまり、 2π ――(x'・cosθ'+y'・sinθ'−ct')=Φ(定数) λ0 となるようなx'とy'は、 x'=a'・cosθ' y'=a'・sinθ' a'=λ0・Φ/2π+ct' です。 すなわち、半径a'の球面(z'はy'と同形なので)になります。これが球面 波の波面を表しています。 この球面波面がS系ではどうなるかというと、 x=a・cosθ y=a・sinθ と表せます。 ではS系でも球面なのか、というと違いますね。比例係数aが定数にはなってい ません。 それは・・・。 (すみません、お腹がすいたので続きは次回に持ち越します・・・)。 | |||
| [danwa:0136] Re: 光行差・ドップラー効果と波面 | ||||
| Date:Tue, 11 Jan 2000 20:19:39 | From: 浜口 | |||
|
浜口です. ([danwa:0134]石坂さん)
しかし,教科書はあくまで教科書にすぎないので,教科書にとらわれずにあ れこれ考えることが,勉強になるんだと思いますよ.(^_^)
(それでも簡単だとは思うが) ささいなことでしたごめんなさい,本題に入ります.
x',y'の1次方程式は平面の方程式ですよ. (もちろんz'は省かれています(x'y'平面での切り口を考えている)) まずは,「光速で広がる球面」を式で表してみましょう. 浜口 | ||||
| [danwa:0144] Re: 光行差・ドップラー効果と波面 | |||||
| Date:Sat, 15 Jan 2000 22:02:36 | From: 石坂 | ||||
|
みなさん、こんばんは。石坂です。 さて、このメールでは以下の2つのことを書いています。 1)光速で広がる球面の式 2)前回の[danwa:0134]で考えた事 [danwa:0136]浜口さん:
x'2+y'2=(ct'+r0)2 (ただし、r0はt'=0での球殻の半径) でいいですか? 2)前回考えた事
[danwa:0110]で浜口さんが x'方向の平面波の式について、
上の式が表す平面上の点で、原点(0,0)に最も近い点は(θ'方向上の) x'=a'・cosθ' y'=a'・sinθ' (ただしa'=λ0・Φ/2π+ct') であり、θ'が任意の値を(連続的に)取る時、この(x',y')群は半径a'の球面と なる(上の式が表す平面群の包絡面は球面)。この球面こそ求める球面波を表して いるのではないか、 そして、この球面上にある点(x'、y')をローレンツ変換したら、S’系で球面だっ た波面が慣性系Sでどう変化したかわかるのではないか、 と考えたのです。方針が間違っていたでしょうか (;_;)? | |||||
| [danwa:0147] Re: 光行差・ドップラー効果と波面 | |||
| Date:Tue, 18 Jan 2000 10:10:24 | From: 浜口 | ||
|
浜口です,こんにちは. ([danwa:0144]石坂さん)
間違ってはいません.その方針でも計算できると思います. うーん,これもまた好みというかセンスの問題なのでどちらがどうというこ とはないんですが,私としては,「球面を平面群の包絡面として表す」よりは, まず単純に「ふつうの球面の方程式を使ってみる」ほうが自然なような気がし ます. (それで,もしダメなら,そのときに別の手を考えればよい) さて,球面の方程式ですが, ([danwa:0144]石坂さん)
(つまり半径が速度cで大きくなっていくということです) ついでに,波長も式の中に表現してしまいましょう. 波長λ0は波面の間隔です.半径の差がλ0になる 同心球面群を式で書けば, x'2+y'2=(ct'+nλ0)2 (nは整数) です.これが「光速で広がる,波面間隔λ0の球面群」の方程式です. (r0は本質的でないので省きました) いよいよ山場です. これをS系で記述するとどうなるでしょうか. (球面にはならないだろう,という石坂さんの予想は当たるか?) 浜口 P.S. じつは,私は当初,平面波のローレンツ変換までしか考えていませんでした. 球面波のローレンツ変換を計算したのは初めてです.石坂さんのおかげで非常 に勉強になりました.感謝.(^_^) | |||
| [danwa:0149] Re: 光行差・ドップラー効果と波面 | ||
| Date:Thu, 20 Jan 2000 16:16:41 | From: 石坂 | |
|
談話室のみなさま、こんにちは。 [danwa:0147] 浜口さんのアドバイスにしたがって、球面波の式
すると、あれー(?_?)思ってもみなかった、とても おもしろい式が出てきました! 計算間違いだといけないので、もう一度検算してから、 結果をご報告いたします。 しばらくお待ちください。 石坂 | ||
| [danwa:0150] Re: 光行差・ドップラー効果と波面 | |
| Date:Fri, 21 Jan 2000 16:07:56 | From: 石坂 |
|
談話室のみなさん、こんにちは。 石坂です。 さて、球面波のローレンツ変換について、いろいろな やり方で計算してみましたが、答が同じになりましたの で、報告します。 ただ、まだ計算間違いがあるかもしれませんし、この 結果をどう解釈したらいいものやら正直とまどっていま す。浜口さんにフォローをお願いできれば、と思います。 #それにしても、浜口さんのご指摘通り、球面波の式を そのままローレンツ変換する方が、球面上の点(x',y') をローレンツ変換してつなぎあわせるより、はるかに計 算が楽でした (^^;)。 簡単のために、球面波の式(念のための注:z'の項は 省略しています) x'2+y'2=(ct'+nλ0)2 (nは整数) の右辺を左辺に移項して、 x'2+y'2−(ct'+nλ0)2=0 ・・・(1) をローレンツ変換することにします。 なぜ簡単かというと、x'2+y'2−(ct')2は ローレンツ不変な量なので計算する必要がなくて、(1)式の 左辺はただちに、 (左辺)=x2+y2−(ct)2 −2nλ0・ct'−(nλ0)2 となり、ローレンツ変換が必要なのはt'の一次の項だけだ からです。ここにt'のローレンツ変換の式 ct'=γ(ct−x・V/c) ____________ :ただしγ=1/√(1−V2/c2) を代入して、tの項、xの項にそれぞれまとめると、出てく るのが、以下のような式です。 (x+γ・nλ0・V/c)2+y2 =(ct+γ・nλ0)2 これは(↑)・・・球です!! 球面波をローレンツ変換したら球面波になっちゃいました。 (もちろん、球の中心は原点ではなく x=−γ・nλ0・V/c ですし、S系で観測される波長はドップラー効果によってλ0 にはならないのですが・・・) [danwa:0101]や[danwa:0134]などで 私が予想していたのは 「光源が運動しているとき、光行差だけ考慮するなら角度の 変換だけなので球面波は球面波のままだが、実際にはローレ ンツ収縮やドップラー効果も一緒に考慮する必要があるので S系での波面は楕円体(大福のような形?)になる」という ものでした。 どこかで計算間違いをしたでしょうか?正しいとすると、 今回の結果をどう理解したらいいのでしょう・・・。 うーむ・・・ <(-_-;)> | |
| [danwa:0151] Re: 光行差・ドップラー効果と波面 | ||||
| Date:Sat, 22 Jan 2000 16:52:58 | From: 浜口 | |||
|
浜口です.こんにちは. ([danwa:0150]石坂さん)
うまい計算だと感心しました.私はもろにx'とt'を代入して,どえらい計 算をしてしまった…….A^_^;;;
ところで,ドップラー効果が何か別のところから導入されるかのような書き ぶりをしておられますが,そうではなくて,この球面の方程式からドップラー 効果が出てくるんですよ. x軸上で球面の間隔λがどうなっているかを計算すれば,ドップラー効果の 公式がすぐに出ます. 「波面の変換がすべてである(ドップラー効果も光行差も波面の変換から自然 に導かれる)」ということが,まだ腑に落ちませんか? 浜口 | ||||
| [danwa:0214] Re: 光行差・ドップラー効果と波面(ドップラー効果のための模型) | |
| Date:Mon, 3 Apr 2000 14:29:00 | From: のりこ |
|
談話室のみなさまへ 元気なのりこです。 おとなしくをこころ掛けているのですが、 メールを拝見しては投稿しそうになっておりました。 相対論をお勉強(?)するのが好きな、 のりこは投稿された、 「光を光速で追う」 「光速度系の時間」 「光行差・ドップラー効果と波面」 を読ませて頂いては真夜中だというのに大笑いしております。 3回読みましたが、また読んでみたいと思ったりします。 実は、昨年のりこは、 ドップラー効果のための模型を作ってしまったのです。 工作は得意でないので簡単なものなんですが。 この模型を生かすことができないかとお勉強していたのです。 同じ長さの赤い針金と青い針金。 粘土を使った台に、 空間を表すための竹ひご。 大きな赤い球と小さな青いの球。 模型の各パーツに名前をつけたいと悩んでいました。 それに模型取り扱い説明を考えていたのです。 赤と青の針金は E=hυ。 針金をくるっとまわすと ω=2πυ。 光はあらゆる方向に進むのだから、 sin波の位相をそろえると、 くるっと丸い針金は球になる。 竹ひごで空間座標あらわせるんでは・・・。 なんて模型を作っているうちに、 ドップラー効果がわかったような気になったのは、 はやとちり ? わぁー 朝ごはんまだ食べてませんでした。 | |
| [danwa:0244] Re: 光行差・ドップラー効果と波面 | |||
| Date:Sun, 4 Jun 2000 19:02:41 | From: 石坂 | ||
|
談話室のみなさま、ご無沙汰しております。石坂です。 光行差・ドップラー効果と波面の話題について、尻切れ トンボみたいになってしまってすみません。 [danwa:0151]浜口さんwrote:
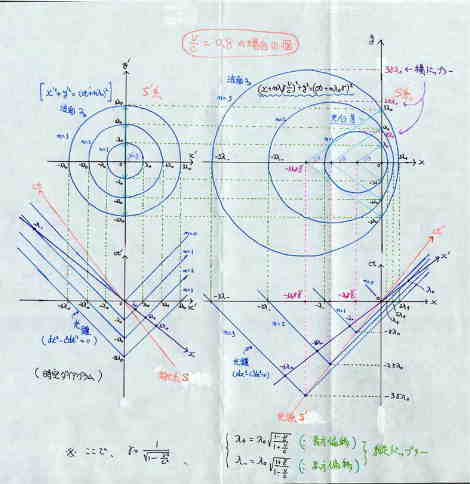
でもやっぱり何かに引っかかります(困ったことだ・・・)。 というわけで、 [danwa:0214]のりこさんwrote:
| |||
| [danwa:0246] Re: 光行差・ドップラー効果と波面 | |||
| Date:Tue, 6 Jun 2000 12:48:03 | From: のりこ | ||
|
談話室のみなさま こんにちは。 のりこです。 [danwa:0244] Re: 光行差・ドップラー効果と波面
だって、 とっても知りたい時にメールを頂いたのだから、 うれしくてお勉強してしまうわけです。 真夜中に大笑いした自分にビックリしたりして (^^) 今は電磁波の正体を知ろうと、 4月から科学館の展示物を見て、 頭の中 いっぱいになってしまったところです。 整理整頓しなきゃ。 光源と一緒に動くS’系と静止系Sでの 波面の時空図とXY空間図ありがとうございます。 | |||
| [danwa:0247] Re: 光行差・ドップラー効果と波面 | ||
| Date:Wed, 7 Jun 2000 02:33:53 | From: 浜口 | |
|
石坂さん,こんにちは. おひさしぶりです.(^_^) ([danwa:0244]石坂さん)
だいぶ時間が経ってしまったので,印象が薄れているのだと思います. あらためてやりとりを最初から読み直すと,石坂さんの問題意識がどこにあ ったのかが,わかると思いますよ. たとえば, 「球面波をローレンツ変換すると(移動する座標系からみると),球面波になる のだろうか?」 なんてのもありましたよね. このことは,納得されましたか? (図までお書きになったくらいなので納得されているとは思いますが) 浜口 | ||
| ・・・さて、この先 話はどうなるのか?お楽しみに!・・・ | |
| 入室希望の方はこちらへ | 『科学談話室』の話題一覧 |
科学あれこれ
ホームページへ